Die Kreiszahl Pi (π)

Der folgende Artikel gibt dir einen kompakten Überblick über die Geschichte der Zahl Pi, ihren mathematischen Eigenschaften und dem Kult, der sich rund um diese geheimnisvolle Zahl entwickelt hat. Und natürlich wird auch die (für jeden Schüler) wohl spannendste Frage beantwortet: Wofür braucht man Pi?

Um eine erste Definition vorwegzunehmen: Der griechische Buchstabe π, ausgesprochen "Pi", bezeichnet jene Zahl, die die Relation von Kreisumfang zu Kreisdurchmesser darstellt. Was das im Detail bedeutet, erfährst Du später noch.
In der Mathematik werden für die wichtigsten Konstanten griechische Buchstaben vergeben. Das erleichtert den Umgang mit ihnen, insbesondere bei Rechenvorgängen, enorm. Denn ansonsten müsste die Zahl jedes Mal erneut ausgeschrieben werden. Bei der unendlich langen Kreiszahl Pi ein unmögliches Unterfangen. Griechische Buchstaben in mathematischen Rechnungen verweisen also immer auf etwas, dass in der Mathematik einen hohen Stellenwert besitzt. Nur die wichtigsten Konstanten verfügen über einen repräsentierenden Buchstaben aus dem griechischen Alphabet.

Pi hat im Laufe der Jahrhunderte unter vielen verschiedenen Begriffen in die Wissenschaft Eingang gefunden. Dazu gehören mit der "Ludolphschen Zahl" und der "Archimedes-Konstante" die wohl noch geläufigsten Synonyme. Bei allen drei Bezeichnungen handelt es sich also um die selbe Zahl von etwa 3,14159.

Die Zahl Pi ausgeschrieben (500 Nachkommastellen)

Anzeigen:

Die Geschichte der Kreiszahl Pi

Die Kreiszahl Pi beschäftigt die Menschheit schon seit mehreren Jahrtausenden. Und dies hat einen einfachen Grund: die Konstruktion von Rädern bringt eine Konfrontation mit dem Verhältnis von Umfang und Durchmesser zwangsläufig mit sich.

Erstmals wirklich schriftlich erwähnt wurde Pi vom griechischen Mathematiker Archimedes (287-212 v. Chr) im dritten Jahrhundert v. Chr. Da sich fortan die Mathematiker auf die Arbeit von Archimedes bezogen, wurde die Zahl "Archimedes-Konstante" genannt. Der Buchstabe Pi aus dem griechischen Alphabet kam erst im späten 18. Jahrhundert erstmalig zum Einsatz. Zwischenzeitlich hieß die Kreiszahl auch "Ludolphsche Zahl", benannt nach Ludolph van Ceulen (1540-1610), der den Großteil seiner Lebenszeit mit der exakten Berechnung der Nachkommastellen von Pi verbrachte.
Während Archimedes hauptsächlich die theoretischen Grundlagen für die unendliche Berechnung der Nachkommastellen lieferte, berechnete van Ceulen die Kreiszahl Pi auf 35 Stellen nach dem Komma. Für diese rein händische Rechnung benötigte er mehr als zwei Jahrzehnte.
Vermutungen legen indessen nahe, dass bereits die alten Ägypter die Zahl Pi zumindest annäherungsweise kannten. Die Maße der Cheops Pyramide (etwa 4500 Jahre alt) wurden in Zusammenhang mit der Kreiszahl gebracht. Bisher konnte dies aber nicht überzeugend wissenschaftlich bestätigt werden.

In der Geschichte der Erforschung der Kreiszahl reihen sich viele namhafte Mathematiker ein. Auch John Wallis, Gottfried Wilhelm Leibniz und Leonard Euler beschäftigten sich mit der Berechnung bzw. der Suche nach neuen Formeln zur schnelleren Bestimmung der Nachkommastellen. Ohne Hilfe von Computern gelang es bis ins frühe 20. Jahrhundert gerade einmal etwa 400 Nachkommastellen zu bestimmen.
Mit der Hilfe von leistungsstarken Computersystemen wird praktisch jährlich ein neuer Rekord gebrochen. Den aktuellen Rekord (Stand 2014) halten Shigeru Kondo und Alexander Yee mit mehr als 12.000.000.000.000 (zwölf Billionen) bestimmten Stellen nach dem Komma.

Woher kommt die Zahl Pi?

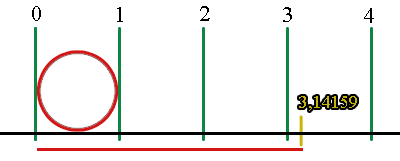Zentrale Aussage: Jeder Kreis mit dem Durchmesser 1 hat den Umfang von Pi (3,14159).
Bildlich kann man es sich in etwa so vorstellen: Man legt mit einer Kordel einen beliebig großen Kreis. Der Durchmesser dieses Kreises besitzt jetzt die Größe 1 (siehe Abbildung). Wenn man den Kreis nun auflöst und die Kordel längs legt, erhält man die Länge des Umfangs, die dem 3,14159fachen Durchmesser entspricht. Das gilt ausnahmslos für alle Kreise sämtlicher Größe.

Dabei mögen jetzt einige einwerfen: "Aber nicht jeder Kreis hat den Durchmesser = 1". Es handelt sich hierbei allerdings um keine feste Maßeinheit, der Kreis könnte ebenso einen Durchmesser von 10cm, 20cm oder 76,52cm haben. (Allein die Relation, also das Verhältnis, zwischen Durchmesser und Umfang ist damit gemeint.) Wenn man diese Zahlen mit Pi multipliziert, erhält man immer den Umfang des Kreises (10cm * π = 31,41cm; 20cm * π = 62,83cm; 76,52cm * π = 240,39cm). Je größer der Durchmesser eines Kreises, desto größer (logischerweise) auch der Umfang und das immer im festen Verhältnis von 3,14159 (π). Aus diesem Grund handelt es sich bei der Kreiszahl um eine universell geltende Naturkonstante.

Merksatz: Jeder Kreis mit dem Durchmesser = 1 hat den Umfang von Pi. Das Verhältnis zwischen Durchmesser und Umfang von 3,14 bleibt immer gleich, ganz egal wie groß der Kreis auch sein mag.

Wofür braucht man Pi? Was kann man mit Pi ausrechnen? Formeln!

Für die gymnasiale Mittel- und Oberstufe ist die Kreiszahl in erster Linie im Zusammenhang mit dem Teilbereich der Geometrie relevant. Mit Pi lassen sich die Kreisfläche, der Kreisumfang, der Durchmesser und der Radius bestimmen. Im Folgenden sind die wichtigsten Formeln dargestellt: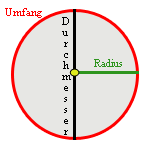

Kreisfläche = (π * Durchmesser²) / 4
Kreisfläche = π * Radius²
Umfang = π * Durchmesser
Umfang = 2 * π * Radius
Durchmesser = √((Fläche * 4) / π)
Durchmesser = Umfang / π
Radius = √(Fläche / π)
Radius = Umfang / 2 * π

Fakten und Wissen rund um die Kreiszahl:

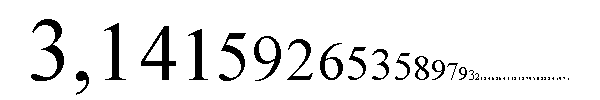
• Pi ist eine mathematische Konstante
• Pi wird definiert als Verhältnis von Umfang zu Durchmesser eines Kreises
• Pi ist eine irrationale Zahl (Pi lässt sich nicht als Bruch darstellen -> Schlussfolgerung: Pi ist unendlich)
• Pi ist eine transzendente Zahl (bedeutet, dass Pi nicht ohne Rest durch ein Polynom dargestellt werden kann)
• Die Zahl Pi ist unabhängig vom Durchmesser/Umfang des Kreises
• Die Zahlen von Pi folgen keinem bestimmten Schema
• Mit dem Bruch 355/113 gelingt eine Annäherung an die Kreiszahl mit sechs richtigen Nachkommastellen